Jenness Enterprises - Statistical Distributions; Cumulative Distribution Functions

Mexican Spotted Owl, stretching...

In general, the Cumulative Distribution Functions return the probability that the Test Value <= X, given that particular distribution.

Distributions
Beta	Chi Square	Logistic	Poisson
Binomial	Exponential	LogNormal	Student's T
Cauchy	F	Normal	Weibull

CDF_Beta: This function returns the probability that the Test Value <= X, assuming a Beta distribution with the specified Shape parameters. This is the Standardized Beta function, where Location = 0 and Scale (upper bound) = 1. According to McLaughlin (2001), parameters Shape1 and Shape2 can be any positive value, but they rarely exceed 10. The function becomes nearly flat if the values get much larger than this.
a) Parameters:
1. Test Value: Number
2. Shape1: Number > 0
3. Shape2: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Beta distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Beta”, {Test Value, Shape1, Shape2}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Beta”, {Test Value, Shape1, Shape2}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Beta", {Test Value, Shape1, Shape2})
c) Function:

CDF_Binomial: The Binomial distribution is used when there are exactly two mutually exclusive outcomes of a trial. This function returns the probability of getting <= X successes out of N trials, given a probability of success = P.
a) Parameters:
1. # Successes: Integer >= 0
2. # Trials: Integer >= 2, # Successes
3. Probability of Success: Number (0 >= p >= 1)
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Binomial distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Binomial”, {#Success, #Trials, Probability of Success}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Binomial”, {#Success, #Trials, Probability of Success}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Binomial", {#Success, #Trials, Probability of Success})
c) Function: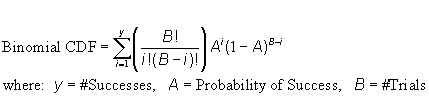

CDF_Cauchy: This function returns the probability that the Test Value <= X, assuming a Cauchy distribution with the specified Location and Scale parameters. The Standardized Cauchy distribution has Location = 0 and Scale = 1.
a) Parameters:
1. Test Value: Number
2. Location: Number
3. Scale: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Cauchy distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Cauchy”, {Test Value, Location, Scale}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Cauchy”, {Test Value, Location, Scale}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Cauchy", {Test Value, Location, Scale})
c) Function:

CDF_ChiSquare: This function returns the probability that the Test Value <= X, assuming a Chi-Square distribution with the specified Degrees of Freedom. The Chi-Square distribution results when v (where v = Degrees of Freedom) independent variables with standard normal distributions are squared and summed (Croarkin & Tobias, Date unknown).
a) Parameters:
1. Test Value: Number >= 0
2. Degrees of Freedom: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Chi Square distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_ChiSquare”, {Test Value, DF}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_ChiSquare”, {Test Value, DF}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_ChiSquare", {Test Value, DF})
c) Function:

CDF_Exp: This function returns the probability that the Test Value <= X, assuming an Exponential distribution with the specified mean. This script uses the 1-parameter version of the equation (i.e. assuming Location = 0). The Standard Exponential Distribution is that which has Mean = 1.
a) Parameters:
1. Test Value: Number >= 0
2. Mean: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Exponential distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Exp”, {Test Value, Mean}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Exp”, {Test Value, Mean}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Exp", {Test Value, Mean})
c) Function:

CDF_F: This function returns the probability that the Test Value <= X, assuming an F distribution with the specified Degrees of Freedom. The F distribution is the ratio of two Chi Square distributions with ratios v₁ and v₂ respectively.
a) Parameters:
1. Test Value: Number >= 1
2. 1st Degrees of Freedom: Number > 1
3. 2nd Degrees of Freedom: Number > 1
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and F distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_F”, {Test Value, DF1, DF2}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_F”, {Test Value, DF1, DF2}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_F", {Test Value, DF1, DF2})
c) Function:

CDF_Logistic: This function returns the probability that the Test Value <= X, assuming a Logistic distribution with the specified mean and scale.
a) Parameters:
1. Test Value: Number
2. Mean: Number
3. Scale: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Logistic distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Logistic”, {Test Value, Mean, Scale}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Logistic”, {Test Value, Mean, Scale}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Logistic", {Test Value, Mean, Scale})
c) Function:

CDF_LogNormal: This function returns the probability that the Test Value <= X, assuming a LogNormal distribution with the specified mean and scale. A LogNormal distribution occurs when natural logarithms of variable X are normally distributed. The Standard LogNormal Distribution is that with Mean = 0 and Scale = 1. The 2-Parameter LogNormal Distribution is that with Mean = 0.
a) Parameters:
1. Test Value: Number >= 0
2. Mean: Number > 0
3. Scale: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and LogNormal distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_LogNormal, {Test Value, Mean, Scale}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_LogNormal, {Test Value, Mean, Scale}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_LogNormal", {Test Value, Mean, Scale})
c) Function:

CDF_Normal_Simpsons: This function returns the probability that the Test Value <= X, assuming a Normal distribution with the specified mean and standard deviation. Because the formula for this function does not exist in a closed form, it must be computed numerically. This script uses the Simpson’s approximation method (Stewart 1998, p. 421-424) to calculate a highly accurate estimate of the Normal cumulative distribution function (accuracy to > 12 decimal places). The Standard Normal Distribution is that with Mean = 0 and Standard Deviation = 1.
a) Parameters:
1. Test Value: Number
2. Mean: Number
3. Standard Deviation: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Normal distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Normal_Simpsons, {Test Value, Mean, St. Dev.}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Normal_Simpsons, {Test Value, Mean, St. Dev.}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Normal_Simpsons", {Test Value, Mean, St. Dev.})
c) Function:

CDF_Poisson: This function returns the probability that the specified Number of Events will be <= X, assuming a Poisson distribution with the specified mean.
a) Parameters:
1. # Events: Integer >= 0
2. Mean: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Poisson distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Poisson, {# Events, Mean}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Poisson, {# Events, Mean}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Poisson", {# Events, Mean})
c) Function:

CDF_StudentsT: This function returns the probability that the Test Value <= X, assuming a Students T distribution with the specified Degrees of Freedom. A Student’s T distribution with 1df is a Cauchy Distribution, and it approaches a Normal distribution when DF>30. Various sources recommend using the Normal distribution if DF>100.
a) Parameters:
1. Test Value: Number
2. Degrees of Freedom: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Student’s T distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_StudentsT, {Test Value, DF}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_StudentsT, {Test Value, DF}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_StudentsT", {Test Value, DF})
c) Function: The CDF_StudentsT T Function is dependent on whether the test value is positive or negative:

CDF_Weibull: This function returns the probability that the Test Value <= X, assuming a Weibull distribution with the specified Location, Scale and Shape parameters. The Standardized Weibull Distribution is that with Location = 0 and Scale = 1. The 2-Parameter Weibull Distribution is that with Location = 0.
a) Parameters:
1. Test Value: Number > Location
2. Location: Number
3. Scale: Number > 0
4. Shape: Number > 0
b) Usages:
1. From "Probability Distribution Calculator", select "Cumulative Probability (CDF)" and Weibull distribution.
2. (Avenue): theProb = av.Run("Jennessent.DistFunc”, {“CDF_Weibull, {Test Value, Location, Scale, Number}})
3. (Avenue): theProb = av.Run("Jennessent.TableDistFunc”, {“CDF_Weibull, {Test Value, Location, Scale, Number}})
4. (Avenue): theProb = av.Run("Jennessent.CDF_Weibull", {Test Value, Location, Scale, Number})
c) Function:

Back to Statistics/Distributions | Summary Statistics | Probability Calculators | References

Calculating Summary Statistics with Avenue

Discussion of Distribution Functions:
Probability Density Functions | Cumulative Distribution Functions | Quantile Functions

Download Statistics Extension Manual (Adobe PDF, version 5)

Please visit Jenness Enterprises ArcView Extensions site for more ArcView Extensions and other software by the author. We also offer customized ArcView-based GIS consultation services to help you meet your specific data analysis and application development needs.